Potency Assays with Partial Curves
Parallelism Between Reference Standard and Test Sample in Potency Tests
Testing for the parallelism (mathematical similarity) of the two regression curves obtained from two bioactive substances is a necessary prerequisite for determining the relative potency of the two substances in biological systems. When the two substances are not parallel (not similar), there is no meaningful relative potency between the reference standard and the test sample. The three methods cited in the USP 1032, 1033, 1034 guidelines for determining the parallelism between substances are the RSSE Chi-Square method (a direct measure of parallelism), the F Test method (a hypothesis test), and the Equivalence method (an empirical test). The dilution series can span a full dose response nonlinear curve or a more limited linear set of doses. The advantage of a full dose response curve is that some differences between substances only appear at high or low doses, and relative potency is more accurately determined. But the more limited number of doses needed for a linear comparison is an advantage for animal studies and requires simpler mathematical computations.
The first two methods utilize the Residual Sum of Squares Error (RSSE) method from regression statistics (also called the Extra Sum of Squares method). The RSSE is the sum of the individual squared residual of each dilution, which is the vertical distance between the observed point and the curve, squared, divided by the estimated variance at that point. These residual methods measure the differences in the RSSEs of the unconstrained fit (independently fit reference standard and test sample curves) and the constrained fit (the two curves constrained to the same shape) to determine parallelism. The curves can be 5PL, 4PL, 3PL, or linear regression models. The parallelism results are either the differences between the constrained and unconstrained RSSEs (RSSE Chi-Square method) or an F test of RSSE ratios (F Test method). A parallelism threshold for the RSSE difference can be established empirically from parallel and nonparallel curve pairs (RSSE Chi-Square method) or from a priori established probability thresholds (RSSE Chi-Square and F Test methods).
The Equivalence method compares the confidence interval limit deltas of the reference standard and test sample of the A and D asymptote coefficients and the B sloping coefficient of 4PL curves or the B slope coefficient of linear regressions. The deltas are either the ratio or differences between the upper and lower limits of each coefficient. The deltas must all fit within defined goalpost borders to be considered parallel. Goalpost borders are established using empirical data from parallel, and sometimes nonparallel also, curve pairs.
The primary difference between the residual methods and the Equivalence method is that the two residual methods (RSSE Chi-Square and F Test methods) compare the individual dilution points of the curves to determine parallelism. The only important criteria are that the dilution points themselves are good fits on their respective unconstrained regressions. The asymptote estimates and slope of the curves are not factors in the parallelism results of the residual methods. In contrast, the Equivalence method compares the asymptote and slope estimates and the individual dilution points of the two curves are not factors in the parallelism results.
While other differences between the three parallelism methods do exist, well behaved assays with full symmetric curves can be handled by all three methods. Differences between the methods arise when the curves do not behave ideally. Some assays have partial curves that don’t reach saturation plateaus within a usable dose range. This makes a reliable estimation of the unsaturated asymptotes in the 4PL problematic for the Equivalence Method. Some assay curves are too asymmetric to be well fit with the symmetric 4PL, resulting in regression curves that have more error between the points and the curve in different regions of the curve. Some assay methods are more ill-behaved, and show more variability between runs than more well-behaved assay methods exhibit.
Goodness of Fit. In regression statistics, it can be shown that the RSSE from an appropriately weighted regression of normally distributed data will be chi-square distributed with number of points minus number of parameter coefficients (N-P) degrees of freedom. This chi-square probability (Fit Prob) applies equally well to all weighted least squares regression fits. The Fit Prob is the likelihood that the computed regression yielded the observed datapoints. For more information about the logistic models and curve weighting, see the Tech Notes: Logistic Curve Weighting.
The Residual Sum of Squares Error (RSSE) Methods For Parallelism Testing
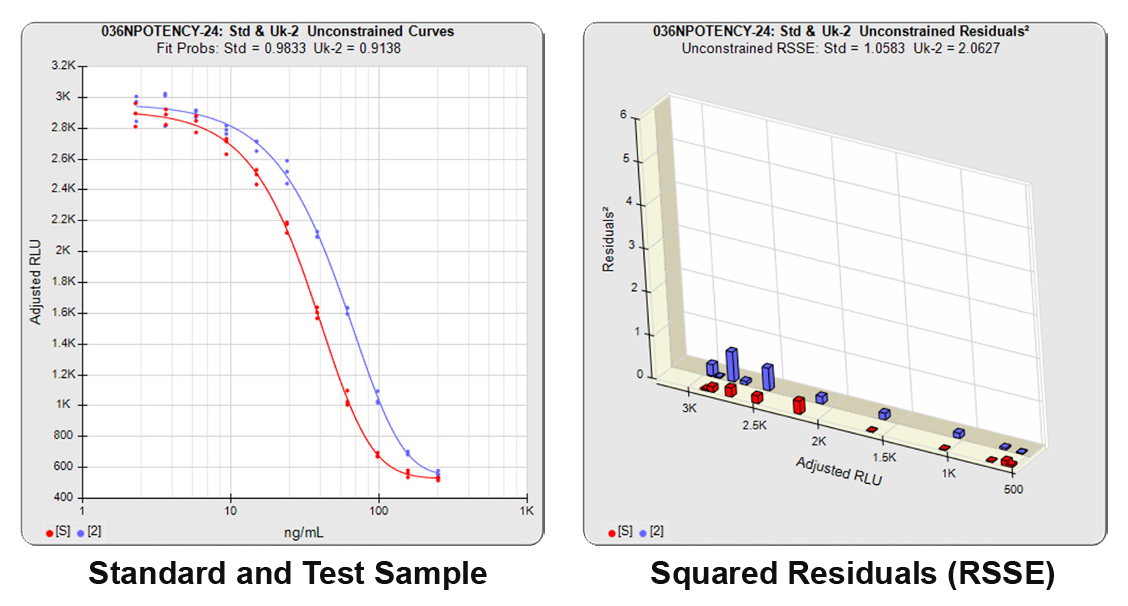
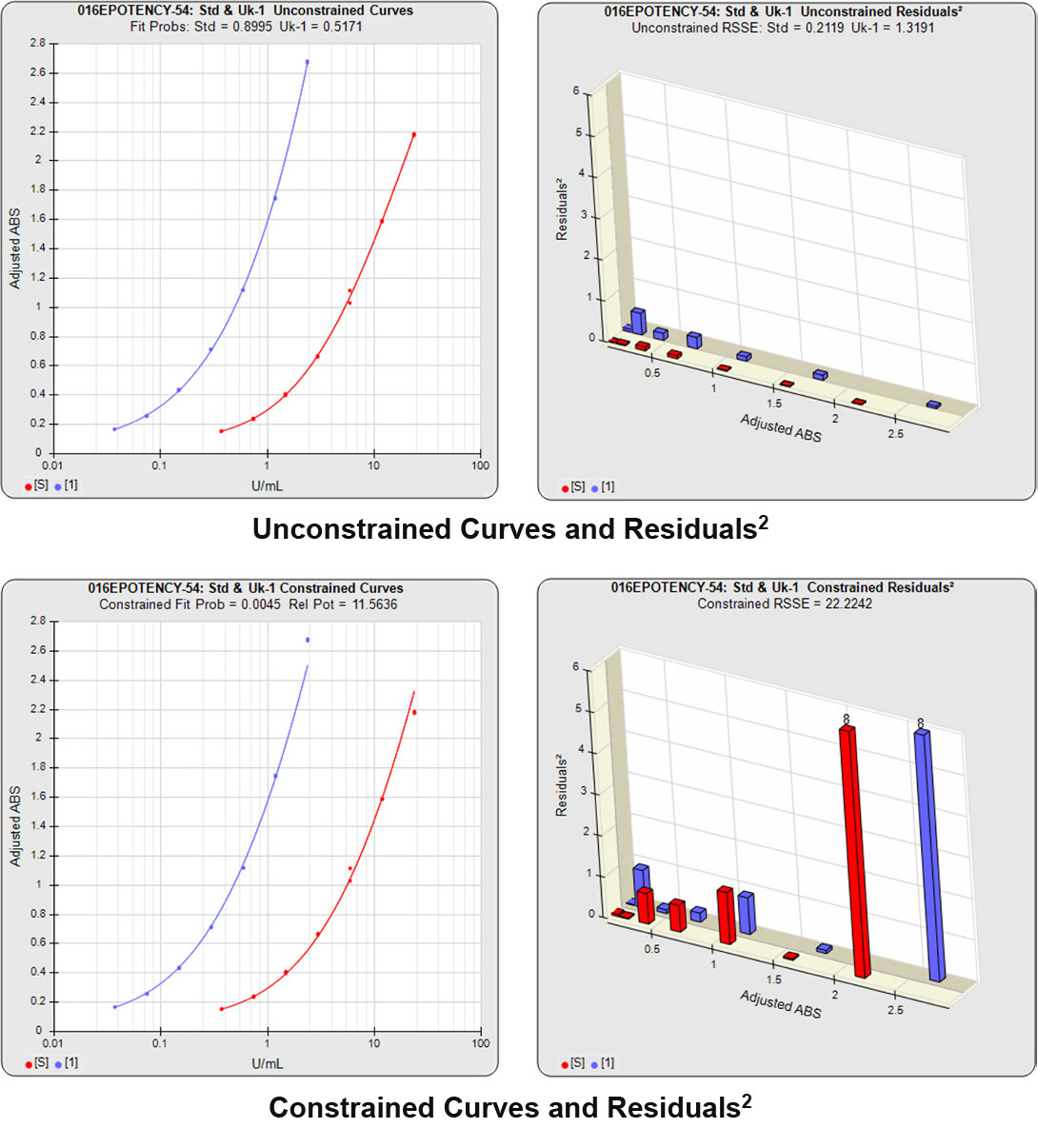
In both Residual Sum of Squares Error methods (RSSE Chi-Square and F Test), the sum of the individual dilution squared residuals (RSSEs) of the unconstrained and constrained regressions are computed. A squared residual is the vertical distance between the observed point and the curve, squared, divided by the estimated variance at that point. In the unconstrained 5PL curves on the left in the graphs above, the data from both curves are computed independently. The individual weighted residuals² between each observed point and its respective curve are plotted on the weighted residuals² graph next to the curves. The sum of these weighted residuals² is the RSSEunconstrained. Since the unconstrained sample responses fit their curves independently, the RSSE’s are not affected by any nonsimilarity (nonparallelism) between the curves. Note that because the residuals² are appropriately weighted, all weighted residuals² are the same scale of magnitude despite the large difference in the scale of the RLU values.
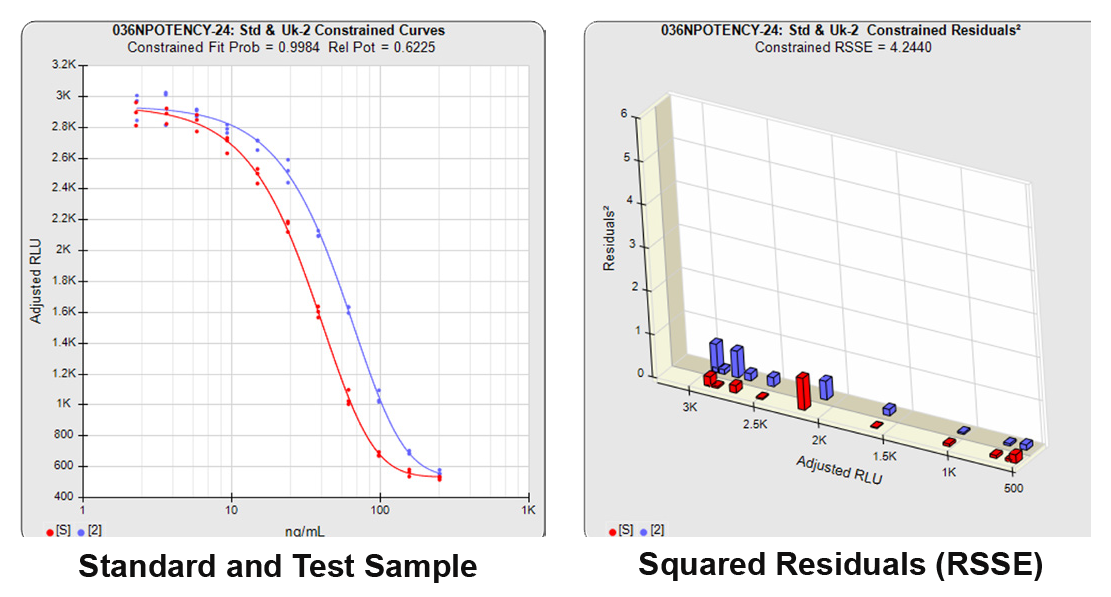
With the constrained curves on the right in the graphs above, the responses from both curves are forced to fit one identical curve shape that provides the best fit for both curves. Since the constrained curves both use the same shape, the RSSEconstrained is affected by the amount of nonsimilarity between the two curves, and consequently have a higher RSSE than the unconstrained curves.
The relative potency is determined from the distance between the two constrained curves.
RSSE Chi-Square Method

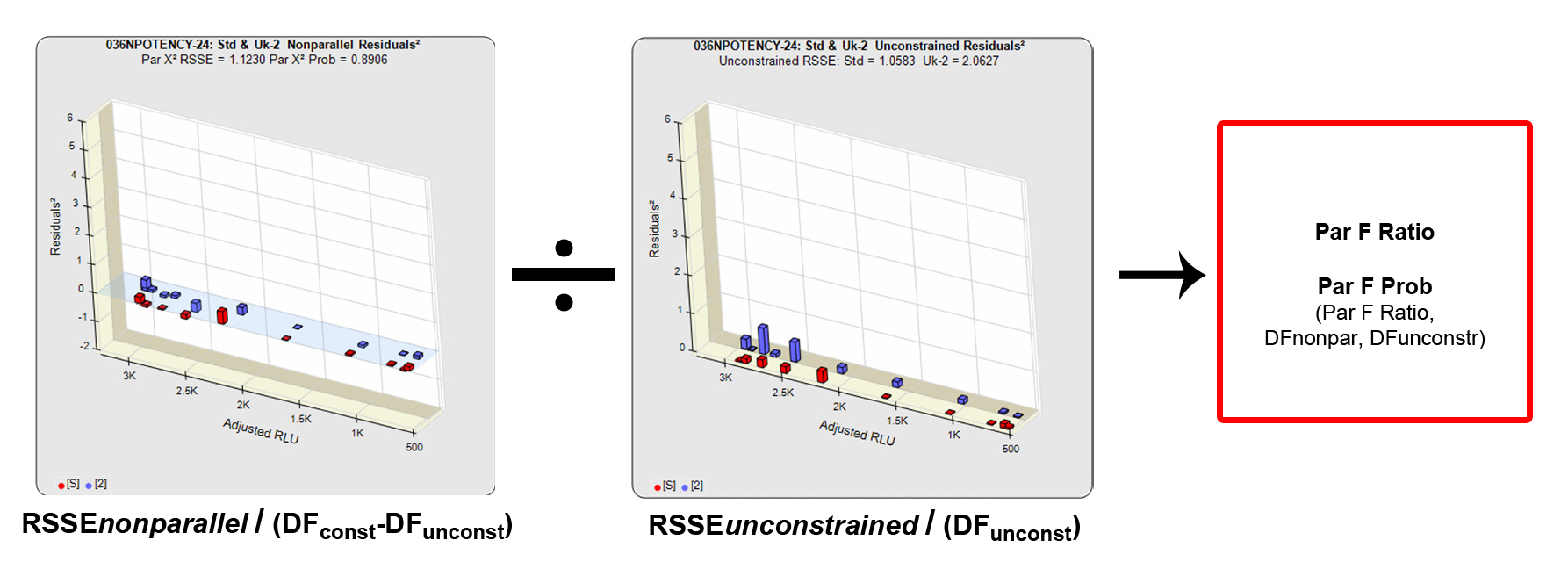
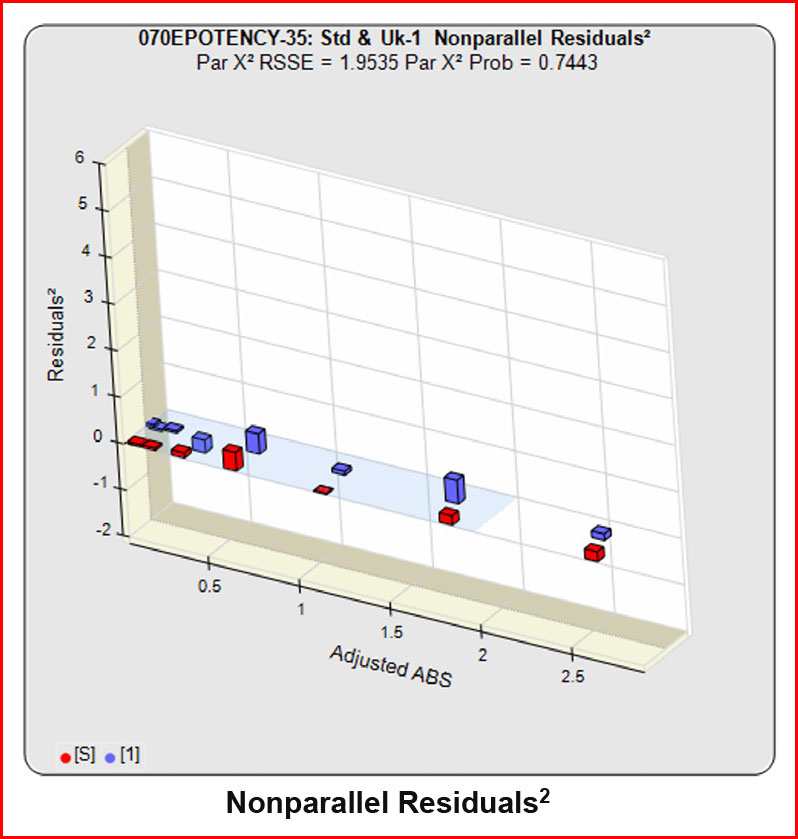
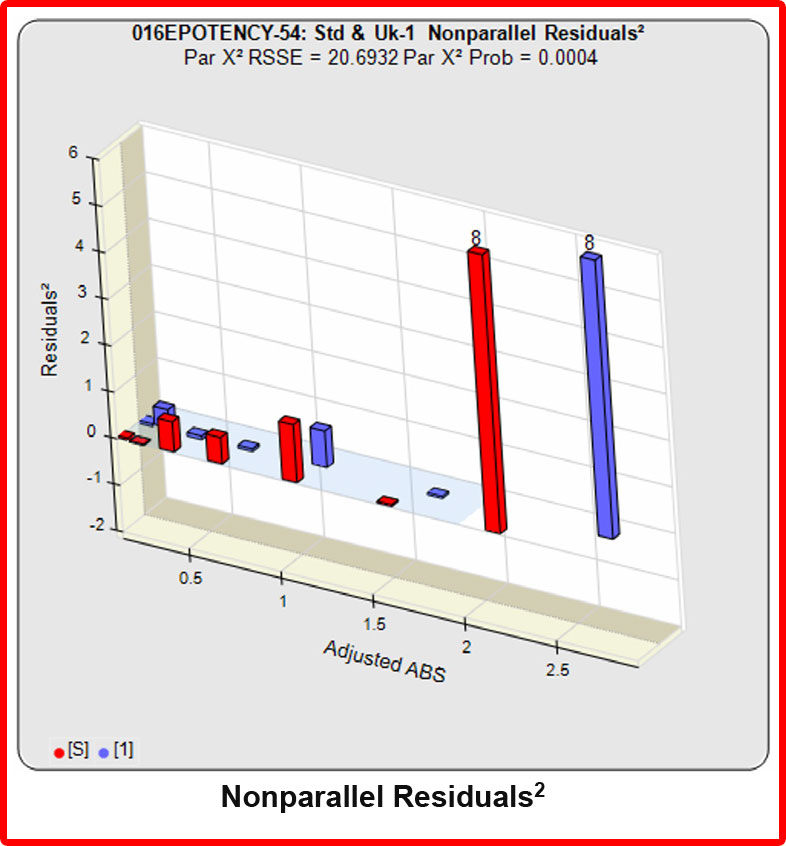
In the RSSE Chi-Square method, the difference between the RSSEconstrained and the RSSEunconstrained shown above is a direct measure of the amount of nonsimilarity (RSSEnonparallel) between the two curves. Any difference between the RSSEconstrained and the RSSEunconstrained , when accurately weighted , is due to the nonsimilarity between the curves. The larger the RSSEnonparallel, the more nonsimilar the curves are to each other. A RSSEnonparallel of zero means the two curves are exactly parallel. The nonparallel residuals² of the individual dilutions also show if any nonsimilarity between two materials is more pronounced at certain dose regions than at other dose regions. Because the RSSEnonparallel (Par χ2 RSSE) is chi-square distributed with P-1 degrees of freedom, a probability (Par χ2 Prob) can also be determined for the curve pair. In the example above, the two materials tested were the same material so the RSSEnonparallel result is minimal.
Note. The RSSE Chi-Square method requires reliable variance estimates of the curve dilutions of that test method. Static weighting formulas like 1/Y and 1/Y 2 are not usable for this parallelism method.
F-Test Method
The sign of b determines the direction of the slope of the 5PL function, and depends upon the order of a and d. Unlike 4PL curves, the order of a and d produce distinct functional shapes in 5PL curves. Most of the sigmoidal shapes that a 5PL can adopt can be formed by both 5PL (a>d) and 5PL (a<d) forms. However, sharp “knees” at transition zones occurring at the upper or lower shoulders of the curve can only be produced by one or the other 5PL form function.
The F Test method was adapted for potency tests by David Finney in his 1978 book “Statistical Methods in Biological Assays” (3rd Edition). Like the RSSE Chi-Square method, the F Test method uses the RSSEnonparallel and RSSEunconstrained from the RSSE Chi-Square method. The F Test method computes a ratio of the RSSEnonparallel / RSSEunconstrained to determine an F probability from that ratio (shown above). A null hypothesis that there is no statistical difference in similarity between the two curves is tested, typically at 0.05 or 0.01 significance. The popularity of the F Test method is that it allows any least squares regression model with full or partial dilution series curves without having accurate weighting models. When accurate weighting is not available, a single estimated variance obtained from all replicate responses is used to compute the residuals². In these cases, it is more reliable when a fairly narrow range of responses are used.
Limitation of F Test
A known weakness of the F Test method for parallelism determinations is that very small RSSEunconstrained from curves that are parallel will generate a failing parallelism probability, and a very large RSSEunconstrained from curves that are not parallel will generate a passing parallelism probability. The RSSE Chi-Square method avoids these limitations. For more information about parallelism testing in potency assays see the Tech Notes: Relative Potency and Parallelism in Potency Bioassays.
Determining a Parallelism Threshold for RSSE Chi-Square Tests
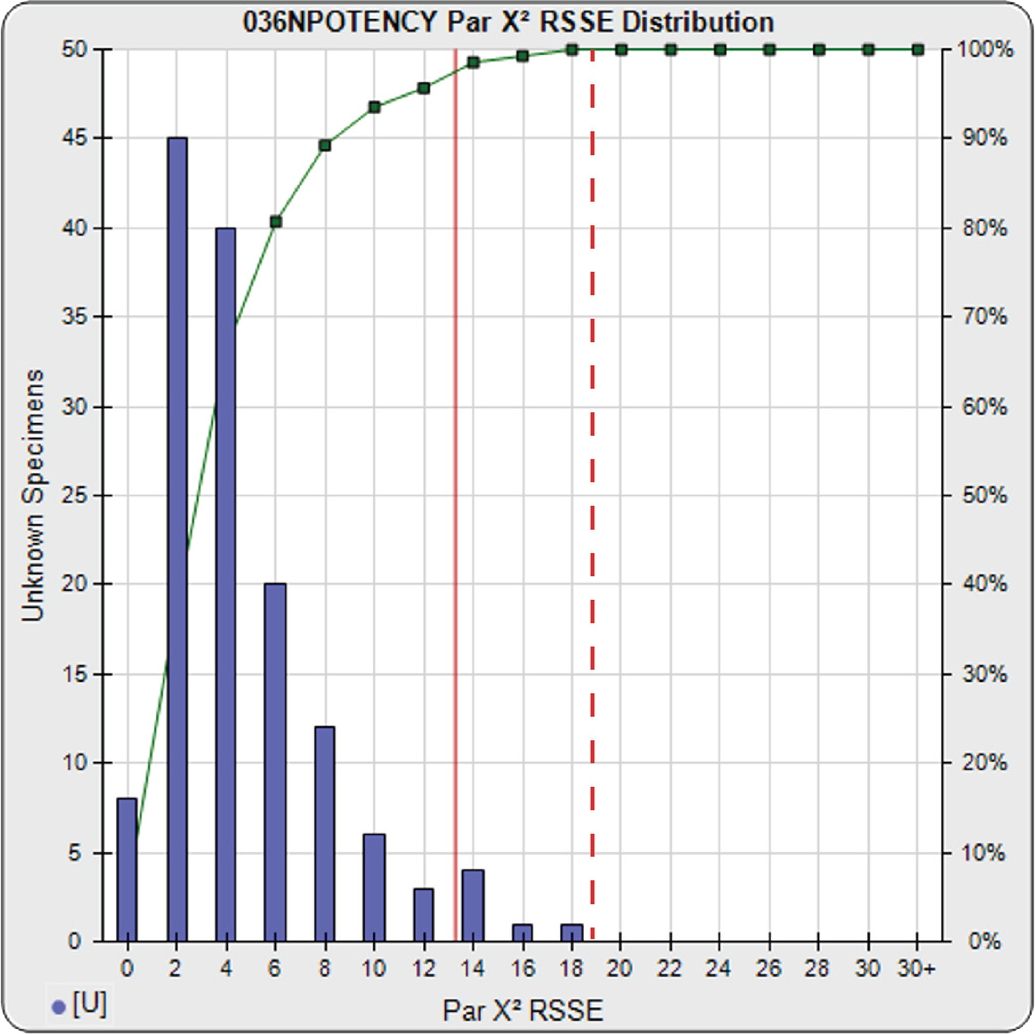
A parallelism threshold for the RSSEnonparallel result in the RSSE Chi-Square method can be set to include any amount of nonsimilarity appropriate for the test. The threshold can be established empirically by computing the RSSEnonparallel from curve pairs that only include test samples identical with the reference standard or with curve pairs that include test samples known to be similar to the reference standard and/or with acceptable amounts of nonsimilarity. In the example to the right, the RSSEnonparallel results from 140 test samples from multiple bioassays of a potency test are plotted against the number of test samples in the histogram. The plots show the characteristic chi-square distribution of RSSE values that result from appropriately weighted regressions, as discussed earlier. Pass/Fail parallelism thresholds can be set to a priori chi square probability limits (0.01 here), as illustrated by the solid red line. The limit can also be set empirically to include an acceptable amount of non-similarity, as illustrated by the dashed red line. These RSSE values are reliable provided the weighting estimates are appropriate and the unconstrained curve fit regressions’ goodness of fits are acceptable.
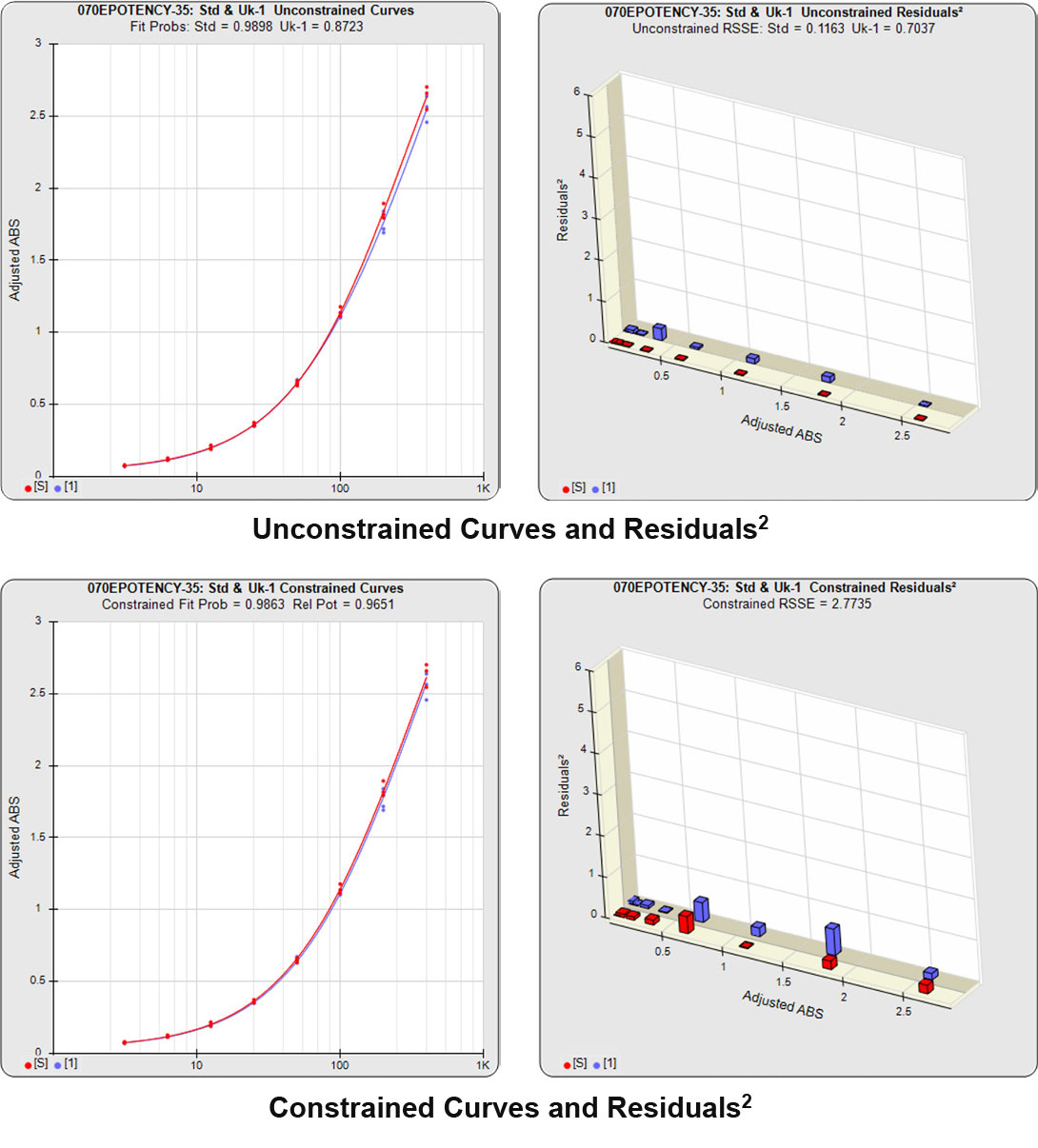
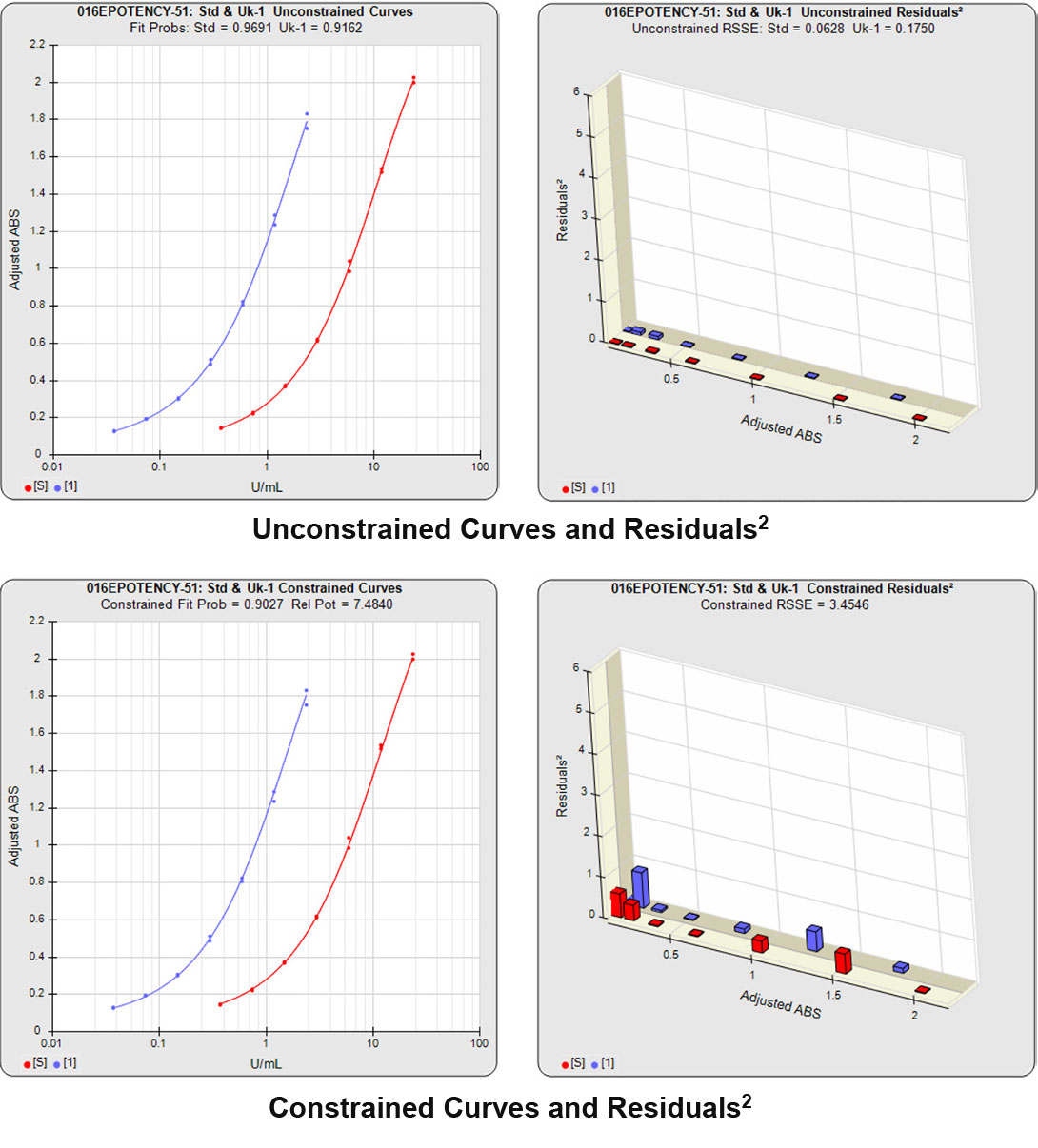
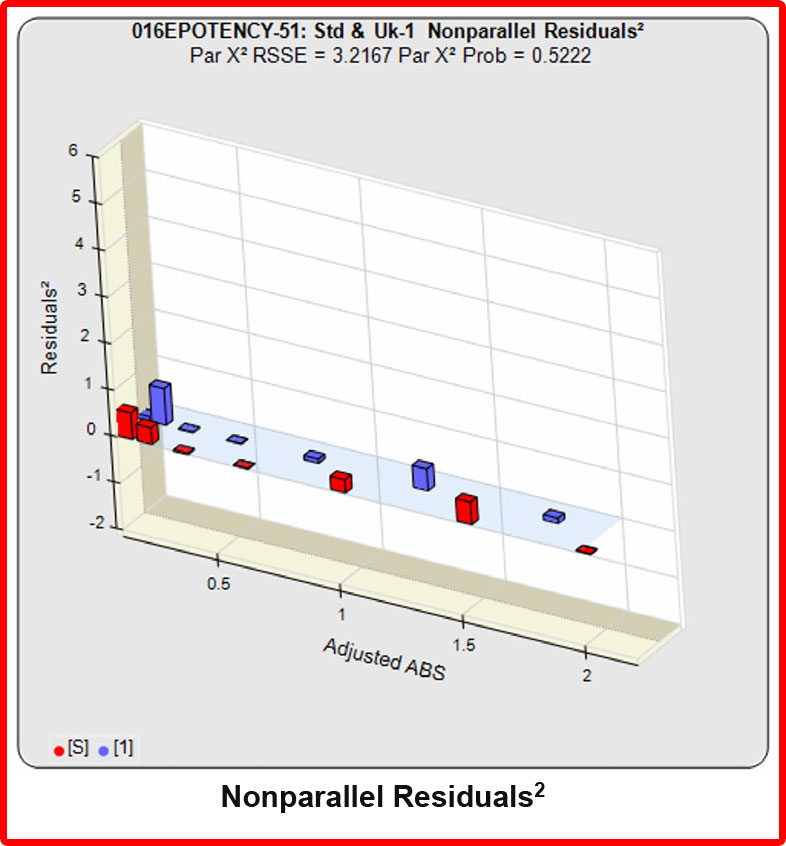
Partial Curves – Example 1
In the first example below, the reference sample and test sample are from a cell-based potency test used for lot release. The curves do not reach an inflection point and a reliable upper asymptote cannot be estimated for either of the curves.
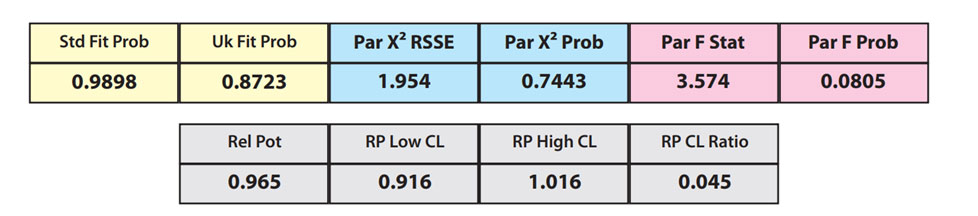
The RSSEunconstrained of the reference standard and the test sample curves were both low indicating good 4PL curve fits. The reference standard Fit Prob was 0.9898 (RSSE = 0.1163) and the test sample Fit Prob was 0.8723 (RSSE = 0.7037). These are highlighted in yellow below.
When the combined RSSEunconstrained is subtracted from the combined RSSEconstrained, the RSSEnonparallel values (Par χ2 RSSE and Par χ2 Prob) show that these two curves are parallel (highlighted in blue). The lower but acceptable F Test probability (highlighted below in pink) is due to the very good curve fits of the two unconstrained curves.
The relative potency and its confidence limits are highlighted below in gray. The RP CL Ratio is the Log10(RP High CL/RP Low CL) ratio. This was within acceptable limits so the relative potency is reportable.
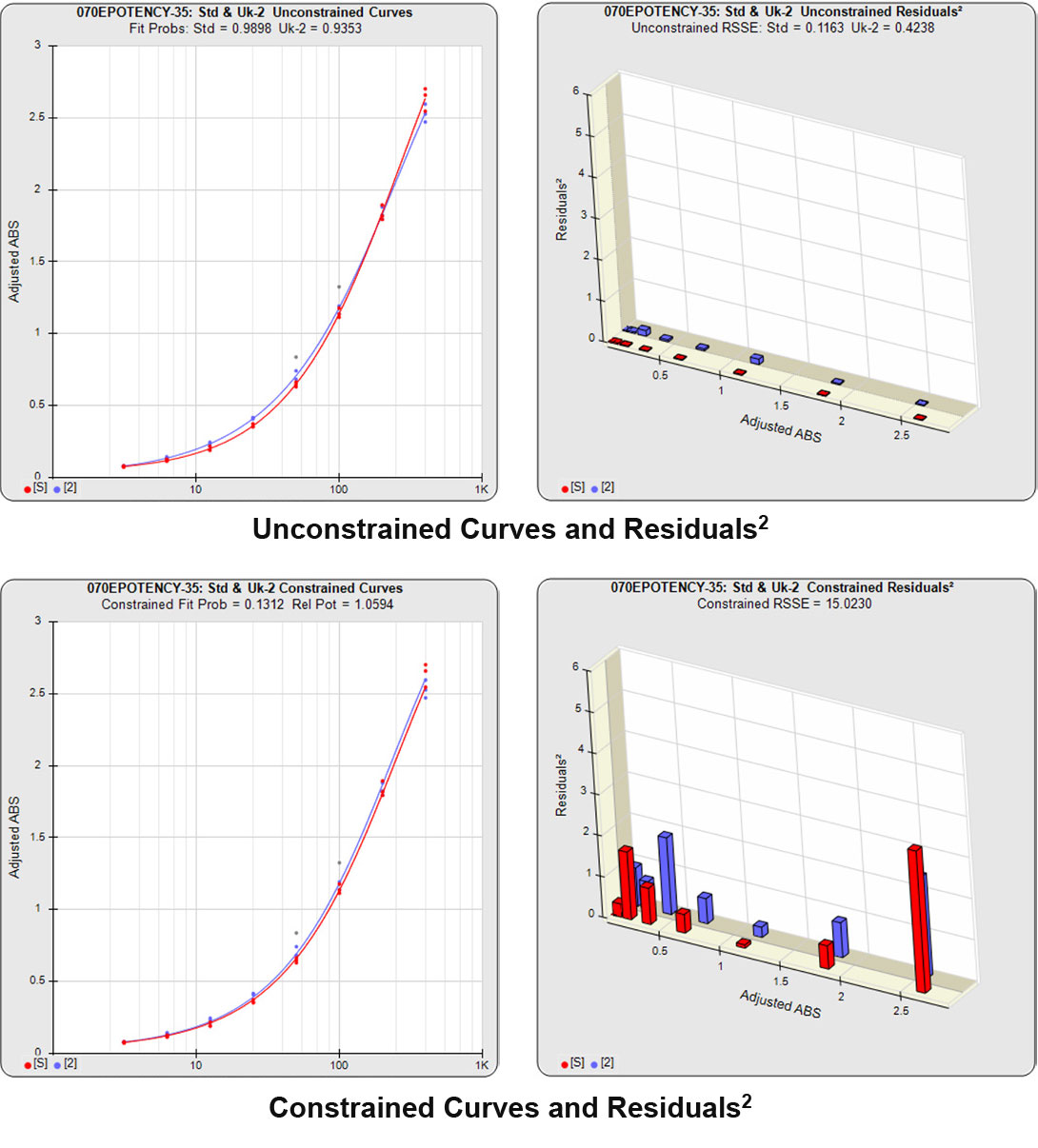
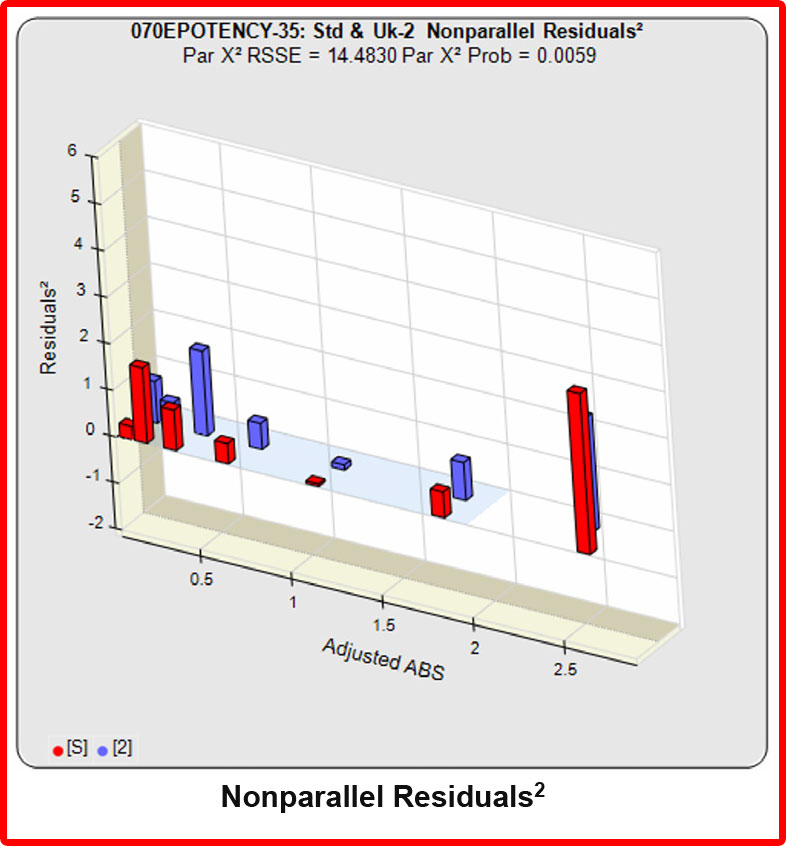
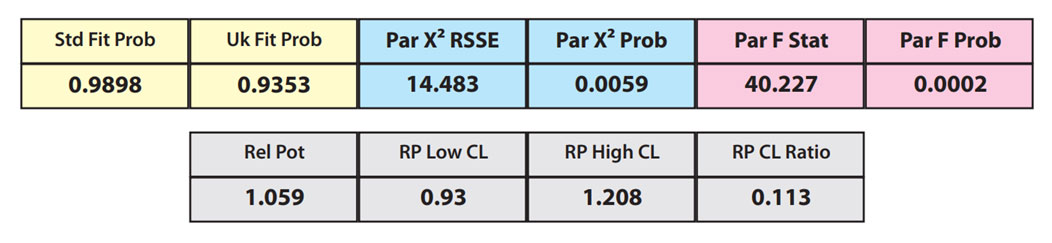
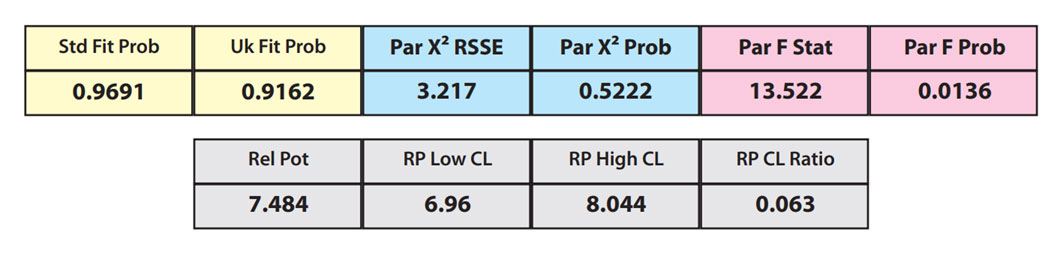
Partial Curves – Example 2
In the second example, the reference sample and test sample are from the same cell-based assay run shown in Example 1.
The RSSEunconstrained of the second test sample curve was low indicating good 4PL fits for both the test sample and reference standard curves.
However, when the combined RSSEunconstrained was subtracted from the combined RSSEconstrained, the Par χ2 RSSE and Par χ2 Prob values show that the second test sample was considerably less parallel to the reference standard than was the first test sample. The two unconstrained curves can be seen to weave around each other in the unconstrained curves graph. The Par F Prob was also extremely low.
Because the test sample was not parallel to the reference standard the two materials are nonsimilar and the relative potency value is not reliable.
Partial Curves – Example 3
In the third example, the reference sample and test sample are from a vaccine test. In this test, parallelism is used to match the antibody species between the two materials.
The RSSEunconstrained of the reference standard and the test sample curves were both low indicating good 4PL curve fits.
When the combined RSSEunconstrained was subtracted from the combined RSSEconstrained, the Par χ2 RSSE and Par χ2 Prob values show that the two curves are parallel. The lower F Test probability is again due to the very good curve fits of the two unconstrained curves.
The confidence limits and RP CL Ratio around the relative potency were within acceptable limits so the relative potency is reportable.
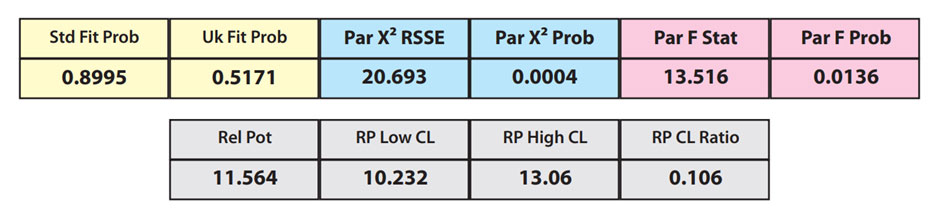
Partial Curves – Example 4
In the fourth example, the reference sample and test sample are from a different run of the same vaccine test shown in Example 3.
The RSSEunconstrained of the second test sample curve was low indicating good 4PL fits for both the test sample and reference standard curves.
However, when the combined RSSEunconstrained was subtracted from the combined RSSEconstrained, the Par χ2 RSSE and Par χ2 Prob values show that the second test sample was considerably less parallel to the reference standard than was the first test sample. The nonsimilarity between the two materials is especially apparent at the high dose regions of the curves. The Par F Prob was also very low.
Since the test sample was not parallel to the reference standard the two materials are nonsimilar and the relative potency value is not reliable.
Conclusion
The Residual Sum of Squares Error (RSSE) method is well established in the regression statistics literature, and its use is widespread in part because of its applicability for testing similarity with all curve types: well-behaved and ill-behaved symmetrical curves, asymmetric curves, and partial curves that do not reach a saturation plateau. For partial curves like those in the examples above, the difficulty of computing a reliable estimate of the unsaturated asymptotes is problematic for the Equivalence Method. Both residual methods, the RSSE Chi-Square method and the F Test, handle all curve types including partial curves because they compare the individual dilution points of the curves to determine parallelism and are not dependent on the asymptotes. These residual methods remain an effective means to assess parallelism for all potency assays. The RSSE Chi-Square method also avoids the weakness that the F Test has with unconstrained curves that have very small or very large RSSEs.
REFERENCES
Bates DM, Watts DG. Nonlinear Regression Analysis and Its Applications. New York: Wiley, 1988.
Belanger BA, Davidian M, Giltinan DM The Effect of Variance Function Estimation on Nonlinear Calibration Inference in Immunoassay Data. Biometrics: 52, 158-175, 1996.
Boulanger B, Devanaryan V, Dewe W, Smith W. Statistical Considerations in Analytical Method Validation. Pharmaceutical Statistics Using SAS: A Practical Guide, 69-94, 2007.
Deming, SN. The 4PL: A Guide to the use of the four-parameter logistic model in bioassay. Statistical Designs, 2015. Draper NR and Smith H. Applied Regression Analysis, 3rd Edition. New York: Wiley, 1998.
Dunn JR, Wild D. Calibration Curve Fitting. The Immunoassay Handbook, Theory and Applications of Ligand Binding, ELISA and Related Techniques, 4th Edition, 323 – 336, 2013.
Finney DL, Phillips P. The Form and Estimation of a Variance Function, with Particular Reference to Immunoassay. Applied Statistics 26, 312-320 (1977).
Finney DJ. Statistical Methods in Biological Assays, 3rd Edition, London: Charles Griffin (1978).
Gottschalk PG, Dunn JR. Determining the Error of Dose Estimates and Minimum and Maximum Acceptable Concentrations from Assays with Nonlinear Dose-Response Curves. Computer Methods and Programs in Biomedicine, 204-215, 2005.
Gottschalk PG, Dunn JR. Measuring Parallelism, Linearity and Relative Potency in Immunoassay and Bioassay Data, Journal of Pharmaceutical Biostatistics 2005, 15 (3), 437–463.
Gottschalk PG, Dunn JR. The Five Parameter Logistic: A Characterization And Comparison With The Four Parameter Logistic. Analytical Biochemistry: 343, 54 – 65, 2005.
Jonkman JF, Sidik K. Equivalence Testing for Parallelism in the Four- Parameter Logistic Model. J. Biopharm. Stat. 19, 2009: 818–837.
Liu JS. Monte Carlo Strategies in Scientific Computing. New York: Springer, 2004.
Seber GAF, Wild CJ. Nonlinear Regression. Hoboken NJ: Wiley, 2003.
Singer R, Lansky DM, Hauck WW. Bioassay Glossary. Stimuli to the Revision Process. Pharmacopeial Forum 32, 2006: 1359–1365.
USP Chapter <1032> Design and Development of Biological Assays. USP Pharmacopeial Convention: Rockville, MD, 2013.
USP Chapter <1033> Biological Assay Validation. USP Pharmacopeial Convention: Rockville, MD, 2013.
USP Chapter <1034> Analysis of Biological Assays. US Pharmacopeial Convention: Rockville, MD, 2013.
Yang H, Kim HJ, Zhang L, Strouse RJ, Schenerman M, Xu-Rong J. Implementation of Parallelism Testing for Four Logistic Model in Bioassays. PDA J. Pharm. Sci. Technol. 66, 2012: 262–269.

www.brendan.com